برش کسری برای حل مسائل عدد صحیح
حل مسائل برنامه ریزی عدد صحیح
تنها تفاوت یک مسئله برنامه‌ریزی عدد صحیح با مسئله برنامه‌ریزی خطی این است که تعداد جواب‌های آن به مراتب کمتر است. در واقع تعداد جواب‌ها تضمین می‌کند که دسترسی به جواب آسان‌تر شود. در واقع عدد متناهی می‌تواند به طور نجومی بزرگ شود. مثلا یک برنامه‌ریزی عدد صحیح با متغیرهای صفر و یک را در نظر بگیرید.
اگر این مسئله دارای n متغیر باشد، تعداد جواب‌های آن 2 به توان n خواهد بود. اگر فقط یک متغیر به مسئله اضافه شود تعداد جواب‌های آن 2 به توان n+1 خواهد شد یعنی تعداد جواب‌های آن دقیقا 2 برابر خواهد شد. از این رو اصطلاحا گفته می‌شود که پیچیدگی مسئله با رشد نمایی است. به همین دلیل است که حتی سریع‌ترین کامپیوتر ها نیز قادر به شمارش همه جواب‌های مسئله که حتی تعداد متغیرها هم کم است نخواهند بود.
این مشکل در مورد حالت کلی یعنی برنامه‌ریزی عدد صحیح جدی‌تر خواهد بود. هرچند الگوریتم‌های پیشرفته‌ای توسعه یافته‌اند به طوری‌که می‌توانند تا حدودی بهتر شمارش عمل نمایند و در بخش‌های بعدی مورد بررسی قرار می‌گیرند ولیکن به علت رشد نمایی پیچیدگی، حتی این الگوریتم‌ها کلا نمی‌توانند مسائلی را حل کنند که تعداد متغیرها زیاد باشند.
نکته مهم: اشتباهی که در مورد آسان بودن حل مسائل برنامه‌ریزی صحیح می‌تواند باشد این است که حذف قسمتی از ناحیه شدنی برنامه‌ریزی خطی (یعنی قسمتی که جواب‌های صحیح در آن وجود ندارد) حل آسان‌تر می‌کند. برعکس، وجود همین جواب‌های شدنی برنامه‌ریزی خطی تضمین می‌کند که جواب بهینه بر یکی از گوشه‌های ناحیه شدنی منطبق باشد (زیرا ناحیه محدب است). نکته مهم در مورد کارایی روش سیمپکلس وجود همین موضوع است.
در نتیجه حل مسائل برنامه‌ریزی خطی به مراتب ساده‌تر از حل مسائل برنامه‌ریزی عدد صحیح است. در نتیجه، موفق‌ترین و بهترین الگوریتم‌های حل مسائل برنامه‌ریزی عدد صحیح در صورت امکان از روش سیمپلکس استفاده می‌کنند. برای انجام این کار قسمت‌هایی از مسئله را که با یک مسئله برنامه‌ریزی خطی متناظر با آن مرتبط می‌سازند (یعنی فرض عدد صحیح بودن متغیرها را کنار می‌گذارند) که اصطلاحا برنامه‌ریزی خطی آزادسازی شده نام دارد.
مسئله P1 که یک مسئله ILP می‌باشد را در نظر بگیرید. مسئله LP آزاد شده آن را که فرض صحیح بودن متغیرهای آن کنار گذاشته شده را هم در نظر بگیرید:
![\[\begin{array}{l} {P_1}:\max Z = Cx\\ Ax \le b\\ x \ge 0,{\mathop{\rm int}} \end{array}\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-3767fc9437f06be57428fc1e9928860c_l3.png "Rendered by QuickLaTeX.com")
![\[\begin{array}{l} {P_1}:\max Z = Cx\\ Ax \le b\\ x \ge 0 \end{array}\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-6a637e5cbe014b7b6884a437fd3b6036_l3.png "Rendered by QuickLaTeX.com")
برای حل مسئله P1 که یک مسئله ILP می‌باشد، مسئله آزاد شده آن یعنی P2 را حل می‌کنیم. اگر جواب بهینه P2 صحیح باشد، که جواب بهینه P1 هم بدست آمده است و بدون آن که مسئله ILP حل کنیم با حل یک مسئله LP جواب بهینه مسئله P1 به دست خواهد آمد.
پس حل یک مسئله ILP با حل یک مسئله LP آزاد شده شروع می‌شود. آن‌گاه بررسی می‌شود که آیا جواب بدست آمده عدد صحیح است یا خیر؟ اگرچه به ندرت اتفاق می‌افتد که جواب بهینه برنامه‌ریزی خطی آزاد شده، عدد صحیح باشد ولیکن در چند حالت خاص چنین اتفاقی می‌افتد.
نکته 1: ناحیه شدنی P1 زیر مجموعه ناحیه شدنی P2 می‌باشد. پس اگر P1 شدنی باشد، حتما P2 هم شدنی است ولی اگر P2 شدنی باشد الزاما P1 شدنی نمی‌باشد. یعنی اگر P2 شدنی باشد ممکن است اصلا نقطه صحیح نداشته باشد و P1 نشدنی باشد.
نکته 2: مقدار بهینه تابع هدف P1 بهتر از مقدار تابع هدف P2 نمی‌باشد.
نکته 3: مسئله P1 می‌تواند جواب بهینه چندگانه داشته باشد ولی هیچ الزامی ندارد که اگر بیش از یک نقطه بهینه داشته باشد حتما بی‌نهایت نقطه بهینه داشته باشد. یعنی در مسائل برنامه‌ریزی عدد صحیح می‌تواند نقاط بهینه بیش از دو نقطه باشد و تعداد نقاط بهینه شمارا باشد.
پیچیدگی محاسباتی مسائل عدد صحیح
تعداد متغیر: با افزایش تعداد متغیرهای مسئله، پیچیدگی مسئله افزایش می‌یابد.
ساختار مسئله: با افزایش تعداد محدودیت‌ها ممکن است حل مسئله ساده‌تر و یا پیچیده‌تر شود. به عبارت دیگر، به طور قطعی نمی‌توان در مورد تعداد محدودیت‌ها و تاثیر آن بر سخت شدن مسئله اظهار نظر کرد.
الگوریتم‌های حل برنامه‌ریزی عدد صحیح
1- الگوریتم برش کسری (برش تمام صحیح)
اگر مسئله برنامه‌ریزی عدد صحیح محض باشد یعنی تمام متغیرها عدد صحیح باشند می‌توان از روش برش کسری استفاده نمود.
مثال: مدل زیر را با استفاده از الگوریتم برش کسری حل نمایید:
پیش‌نیازها: روش سیمپلکس و روش سیمپلکس دوگان
![\[\begin{array}{l} \max z = 7{x_1} + 9{x_2}\\ - {x_1} + 3{x_2} \le 6\\ 7{x_1} + {x_2} \le 35\\ {x_1},{x_2} \ge 0,{\mathop{\rm int}} \end{array}\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-8e8a5238c0ae36c78013f700d4f440dc_l3.png "Rendered by QuickLaTeX.com")
حل: ابتدا مسئله LP آزاد شده را حل می‌کنیم با استفاده از سیمپلکس:
طبق تست مینیمم نسبت‌ها، S1 خارج شوند و x2 وارد شونده می‌باشد.
جدول بالا، جدول نهایی روش سیمپلکس می‌باشد، که پاسخ متغیرها به صورت عدد صحیح در نیامده‌اند. به همین منظور بایستی با اضافه کردن برش به جدول فوق سعی کنیم جواب‌ها را صحیح نماییم.
نوشتن برش برای سطر اول:
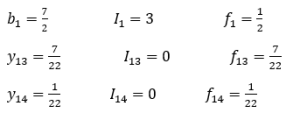
برش را می‌توان به صورت زیر نوشت:
![\[\begin{array}{l} {f_1} - ({f_{13}}{S_1} + {f_{14}}{S_2}) \le 0\\ \frac{1}{2} - (\frac{7}{{22}}{S_1} + \frac{1}{{22}}{S_2}) \le 0 \end{array}\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-25963e39c3b5a49c2c1553a44a8fa456_l3.png "Rendered by QuickLaTeX.com")
برش بالا را به جدول اضافه می‌کنیم:
![\[\frac{1}{2} - (\frac{7}{{22}}{S_1} + \frac{1}{{22}}{S_2}) + {S_3} = 0\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-74f4f81de106faea08300136e10b6e17_l3.png "Rendered by QuickLaTeX.com")
همانطور که در جدول بالا مشخص است مقدار S3 منفی شده است، که باید از روش سیمپلکس دوگان برای حل استفاده نمود.
وارد شوند: s1، خارج شونده: s3
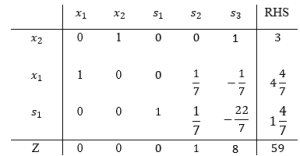
در جدول بالا هنوز متغیر x1 مقدارش صحیح نشده است، پس نیاز است که یک برش دیگر برای سطر دوم نیز بنویسیم و به جدول فوق اضافه کنیم.
![\[\begin{array}{l} \frac{4}{7} - (\frac{1}{7}{S_2} + \frac{6}{7}{S_3}) \le 0\\ \frac{4}{7} - (\frac{1}{7}{S_2} + \frac{6}{7}{S_3}) + {S_4} = 0 \end{array}\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-99f05f5c3fe4928b0c2d477f34efdd31_l3.png "Rendered by QuickLaTeX.com")
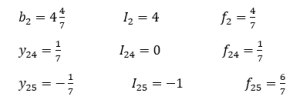
برش بالا را به جدول اضافه می‌کنیم:
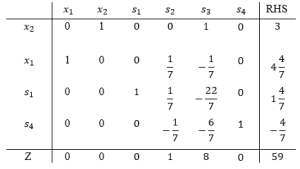
طبق تست مینیم نسبت‌ها، متغیر s4 خروجی و متغیر s2 ورودی می‌باشد.
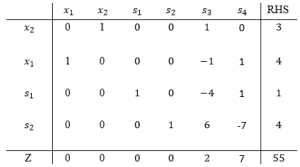
در جدول بالا، تمام متغیرهای عدد صحیح شده‌اند که جواب نهایی مسئله بدست آمده است.
قوت برش کسری
در روش برش کسری، اینکه کدام سطر را برای اضافه کردن برش انتخاب کنیم دارای اهمیت می‌باشد، زیرا ممکن است در سریع‌تر رسیدن به جواب کمک کند.
قاعده اول: به طور کلی طبق تجربه، در روش برش کسری، برشی قوی‌تر است که میزان اعشار بیشتری داشته باشد. مثلا در مثال قبل یعنی جدول زیر، اعشار هر دو سطر یکسان و برابر 0.5 است. در این حالت نمی‌توان تصمیم گرفت که یا می‌توان به صورت تصادفی یک سطر را برای برش انتخاب کرد و یا طبق قاعده دوم که در ادامه توضیح داده می‌شود می‌توان استفاده نمود.
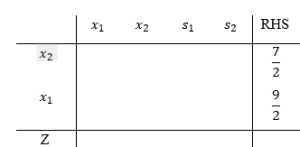
قاعده دوم: سطری انتخاب می‌شود که مقدار رابطه زیر برای آن بیشتر باشد
![\[\max (\frac{{{f_i}}}{{\sum\limits_j^{} {{f_{ij}}} }}),\forall i\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-a32e4397ab56f838603c424291c85402_l3.png "Rendered by QuickLaTeX.com")
یعنی برای جدول مثال قبل داریم:
![\[\begin{array}{l} {x_2} \to \frac{{\frac{1}{2}}}{{\frac{7}{2} + \frac{1}{{22}}}}\\ {x_1} \to \frac{{\frac{1}{2}}}{{\frac{{21}}{{22}} + \frac{3}{{22}}}} \end{array}\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-e0e462326f2b86e59b6bd194cb7be719_l3.png "Rendered by QuickLaTeX.com")
پس سطر x2 برای برش انتخاب می‌شود زیرا مقدار آن طبق رابطه بالا بیشتر است.
بسیار عالی و مفید بود