روش بالاس و برنامه ریزی صفر و یک
برنامه‌ریزی صفر و یک
هر متغیر صحیح که کراندار باشد را می‌توان به صورت متغیرهای صفر و یک نوشت. ساده‌ترین حالت آن می‌تواند به این صورت باشد که اگر
![\[0 \le x \le u\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-d218817b07c7cb3ff864cb878d32d15c_l3.png "Rendered by QuickLaTeX.com")
صحیح باشد، که در آن u یک کران بالا برای متغیر x است. x را می‌توان به صورت زیر نوشت:
![\[x = {y_1} + {y_2} + ... + {y_n}\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-4986f7c2ca1fe1f335534dd4d371e82e_l3.png "Rendered by QuickLaTeX.com")
که در آن y ها صفر و یک هستند. ولی این روش، روش مناسبی برای نشان دادن یک متغیر صحیح به صورت صفر و یک نمی‌باشد، زیرا تعداد متغیرهای صفر و یک مسئله زیاد می‌باشند. به عنوان مثال فرض کنید
![\[0 \le x \le 10000\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-da19c5a2472eae772c5cc51fbf5cc858_l3.png "Rendered by QuickLaTeX.com")
باشد آن‌گاه رابطه قبل به صورت زیر در خواهد آمد:
![\[x = {y_1} + {y_2} + ... + {y_{10000}}\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-d4ebe77bba60710a173ac801974d50c4_l3.png "Rendered by QuickLaTeX.com")
روش دیگر (بهتر)، نمایش متغیر x به صورت زیر می‌باشد.
![\[x = {y_0} + 2{y_1} + {2^2}{y_2} + ... + {2^k}{y_k}\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-bec5c1b716f8bd22c5816c833e2293ef_l3.png "Rendered by QuickLaTeX.com")
که در آن y ها صفر و یک هستند. و در آن k کوچک‌ترین عدد صحیحی است که در رابطه زیر صدق کند:
![\[{2^{k + 1}} - 1 \ge u\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-28655e809be86651edae55e74481bb63_l3.png "Rendered by QuickLaTeX.com")
به عنوان مثال، فرض کنید
![\[0 \le x \le 7\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-b833b9d671e863e8a80b180cafa0046a_l3.png "Rendered by QuickLaTeX.com")
باشد، ابتدا بایستی k را بدست آوریم. کوچک‌ترین k ای که می‌توان بدست آورد که در رابطه بالا صدق کند برابر 2 می‌باشد.
پس داریم:
![\[x = {y_0} + 2{y_1} + {2^2}{y_2}\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-125000ad331994be4b77ea5a9b091080_l3.png "Rendered by QuickLaTeX.com")
مثال: فرض کنید در یک مسئله IP متغیرهای عدد صحیح وجود دارد. با استفاده از محدودیت‌های موجود در مسئله به این نتیجه رسیده‌ایم که
![\[x \le 137\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-9580391340eaeabd0afe753c2e2781ad_l3.png "Rendered by QuickLaTeX.com")
پاسخ:
![\[{2^{k + 1}} - 1 \ge 137 \to k = 7\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-5697f35241564c791e62ca3bdd712bde_l3.png "Rendered by QuickLaTeX.com")
پس داریم:
![\[x = {y_0} + 2{y_1} + 4{y_2} + 8{y_3} + 16{y_4} + 32{y_5} + 64{y_6} + 128{y_7}\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-5746ea676894ae9c45b3ee0daafa3d71_l3.png "Rendered by QuickLaTeX.com")
الگوریتم حل مسائل صفر و یک
الگوریتم جمعی (روش بالاس، شمارش ضمنی)
برای استفاده از روش بالاس بایستی یکسری شرایط در مسئله حتما برقرار باشد، در صورت برقرار نبودن با یکسری تغییرات می‌توان شرایط مد نظر را ایجاد کرد.
شرایط اولیه حل مسائل با روش بالاس آن است که تمام متغیرها بایستی صفر و یک باشند، مسئله باید حتما max سازی و ضرایب تابع هدف همگی منفی (کمتر مساوی صفر) باشند. همچنین محدودیت‌ها باید حتما از جنس کمتر مساوی باشند، در غیر اینصورت با ضرب منفی می‌توان آن را درست کرد.
نکته: اگر ضرایب تابع هدف مثبت بود آن را با
![\[1 - x'\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-d5a6cbd8c3c95ff6ab08ef0664013629_l3.png "Rendered by QuickLaTeX.com")
تعویض می‌کنیم.
مثال: مسئله زیر را با استفاده از روش بالاس حل نمایید.
![\[\begin{array}{l} \max z = - 10{x_1} - 20{x_2} - 30{x_3}\\ 3{x_1} - 5{x_2} - 2{x_3} \le - 6\\ - 2{x_1} - 8{x_2} - {x_3} \le - 7\\ {x_1},{x_2},{x_3} \in \{ 0,1\} \end{array}\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-a6d55b2bde890bdfb78c58df5739a94a_l3.png "Rendered by QuickLaTeX.com")
پاسخ: شرایط مد نظر در مسئله بالا برقرار است. به عبارت دیگر، تابع هدف از جنس حداکثرسازی است و ضرایب تمام متغیرها در تابع هدف منفی هستند.
گام اول: در قدم اول، تمام متغیرها را مقدار صفر قرار می‌دهیم تا بهترین جواب بدست آید. طبیعی است که بهترین جواب مسئله بالا حالتی است که تمام متغیرها مقدار صفر بگیرند. زیرا ضرایب تمام متغیرها در تابع هدف منفی است و از طرفی مسئله حداکثرسازی است، پس دوست ندارد که متغیری مقدار بگیرد.
در این حالت درست است که بهترین جواب مسئله است، اما جواب شدنی نمی‌باشد زیرا در محدودیت‌ها صدق نمی‌کند، به عبارت دیگر داریم:
![\[\begin{array}{l} 0 \le - 6\\ 0 \le - 7 \end{array}\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-da0490aadc7588c7ab2ec28d057d429b_l3.png "Rendered by QuickLaTeX.com")
که درست نمی‌باشند یعنی صفر از 6- و 7- کوچکتر نیست.
پس چاره چیست؟ بایستی متغیرهای مسئله را طوری مقدار یک بدهیم که اولا مقدار تابع هدف بد نشود، از طرفی محدودیت‌ها شدنی باشند.
![\[\begin{array}{l} 0 + {s_1} = - 6 \to {s_1} = - 6\\ 0 + {s_2} = - 7 \to {s_2} = - 7 \end{array}\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-6e0e78442b84ebbc1194c2e7feb2b0f5_l3.png "Rendered by QuickLaTeX.com")
پس ما باید کاری کنیم که متغیرهای اسلک یعنی s1 و s2 بزرگتر از صفر شوند تا محدودیت‌ها شدنی شوند.
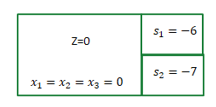
گام دوم: ما باید از بین متغیرهای مدل، یک متغیر را انتخاب کنیم و برای شاخه‌زنی از آن استفاده کنیم. بهتر است متغیری برای شاخه زنی انتخاب شود که مقادیر اسلک را بتواند بیشتر به سمت مثبت شدن پیش ببرد. حال به بررسی هر سه متغیر می‌پردازیم:
![\[\begin{array}{l} 3{x_1} - 5{x_2} - 2{x_3} + {s_1} = - 6\\ - 2{x_1} - 8{x_2} - {x_3} + {s_2} = - 7 \end{array}\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-78f5102acdb80df82651ffb02a635866_l3.png "Rendered by QuickLaTeX.com")
اگر به جای هر کدام از متغیرها، مقدار یک را قرار بدهیم، مقادیر s ها به صورت جدول زیر خواهند بود:
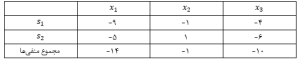
آن متغیری بهتر است انتخاب شود، که مجموع s1 و s2 آن نزدیک صفر باشد. یعنی بتواند بهتر مقادیر اسلک را مثبت کند. پس متغیر x2 انتخاب می‌شود.
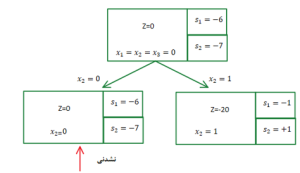
شاخه سمت چپ به این خاطر نشدنی است (بسته شده است) که ما حتی اگر دو متغیر باقی مانده دیگر را هم مقدار یک بدهیم، محدودیت‌ها شدنی نخواهند شد. شاخه سمت راست هم هنوز s1 منفی است، پس باید هنوز شاخه زنی را ادامه بدهیم.
![\[\begin{array}{l} 3{x_1} - 2{x_3} + {s_1} = - 1\\ - 2{x_1} - {x_3} + {s_2} = 1 \end{array}\]](https://optimamooz.com/wp-content/ql-cache/quicklatex.com-ad2235244b37c2be2aeb6f39f7e3eb95_l3.png "Rendered by QuickLaTeX.com")
پس بهتر است متغیر x3 را برای شاخه زدن انتخاب کنیم.
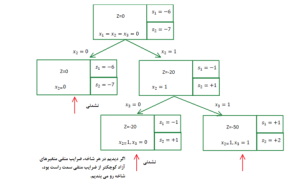
جواب بهینه و نهایی مسئله، بدست آمد.
زیرا در شاخه زیر، مقادیر اسلک همگی مثبت شده‌اند و از طرفی سایر شاخه‌ها هم بسته شده‌اند.
0
9