یا

ساخت حساب کاربری

سبد خرید0

دسته بندی موضوعات

مهندسی صنایع

آموزش برنامه‌ ریزی عدد صحیح – تکنیک‌ های مدل‌ سازی ریاضی

برنامه ریزی عدد صحیح و آموزش یکسری از تکنیک ها مدل سازی ریاضی

مدل ریاضی برنامه‌ ریزی عدد صحیح همان مسئله برنامه‌ریزی خطی است که فقط محدودیت مربوط به عدد صحیح بودن حداقل یکی از متغیرها به آن اضافه شود. در مسائل برنامه‌ریزی عدد صحیح اگر فرض صحیح بودن برای تمام متغیرها موجود باشد آن را برنامه‌ریزی عدد صحیح محض می‌نامیم. اما اگر فرض عدد صحیح بودن برای متغیرها فقط برای برخی از متغیرها باشد آن را برنامه‌ریزی عدد صحیح مختلط می‌نامیم.

هر تصمیمی که فقط دو انتخاب داشته باشد را می‌توان برحسب متغیرهایی بیان کرد که فقط دو مقدار، یعنی صفر یا یک را انتخاب می‌کنند. از این رو متغیر تصمیم از نوع بله یا نه را با xj نشان می‌دهیم به طوری که:

${x_j} = \left\{ \begin{array}{l} 1 \hspace{5pt} {\rm{ if \hspace{5pt} j \hspace{5pt} yes}}\\ 0 \hspace{5pt} {\rm{ if \hspace{5pt} j \hspace{5pt} no}} \end{array} \right.$

نمونه‌ای از مسئله برنامه‌ریزی عدد صحیح محض

Integer Programming (IP)

$\begin{array}{l} MaxZ = 2{x_1} + 4{x_2}\\ 3{x_1} + 2{x_2} \le 30\\ {x_1},{x_2} \ge 0,{\mathop{\rm int}} \end{array}$

در این‌گونه مسائل، تمام متغیرها بایستی از نوع عدد صحیح (integer) باشند.

نمونه ای از مسئله برنامه ریزی عدد صحیح مختلط

Mixed Integer Programming (MIP)

$\begin{array}{l} MaxZ = 5{x_1} + 7{x_2}\\ 2{x_1} + 3{x_2} \le 30\\ {x_1},{x_2} \ge 0,{x_2} \hspace{5pt} {\rm{ is }}\hspace{5pt} {\mathop{\rm int}} \end{array}$

در این‌گونه مسائل، برخی از متغیرها می‌توانند عدد صحیح و برخی نیز پیوسته باشند. یعنی هر دو نوع در مسئله حضور دارند.

نمونه‌ای از مسئله برنامه‌ریزی عدد صحیح صفر و یک

Zero-One programming

$\begin{array}{l} MaxZ = 5{x_1} + 7{x_2}\\ 2{x_1} + 3{x_2} \le 30\\ {x_1},{x_2} \in \{ 0,1\} \end{array}$

در این‌گونه مسائل، تمام متغیرها بایستی از نوع باینری یا صفر و یک باشند.

نمونه‌هایی از فرموله کردن مسئله با متغیرهای صفر و یک

در بعضی از مسائل ILP متغیرهای تصمیم مسئله متغیرهای صحیح می‌باشند و کافی است آن‌ها را در آخر مدل‌سازی صحیح قرار دهیم که این سبک مسائل عدد صحیح را به عنوان نمونه بررسی خواهیم کرد.

محدودیت‌های این یا آن

فرض کنید بخواهیم از بین دو محدودیت زیر همواره فقط یکی از آن‌ها برقرار باشد. یعنی همواره فقط یکی از آن‌ها را بخواهیم استفاده کنیم.

$\left\{ \begin{array}{l} {x_1} + 2{x_2} \le 20\\ 3{x_1} + {x_2} \le 40 \end{array} \right.$

برای این منظور، محدودیت‌های بالا را به صورت زیر بازنویسی می‌کنیم که در آن M یک عدد خیلی بزرگ می‌باشد:

$\begin{array}{l} \left\{ \begin{array}{l} {x_1} + 2{x_2} \le 20 + M{y_1}\\ 3{x_1} + {x_2} \le 40 + M{y_2} \end{array} \right.\\ {y_1},{y_2} \in \{ 0,1\} \end{array}$

محدودیت‌های بالا بیان می‌کنند که از بین دو محدودیت، تنها یک محدودیت می‌تواند برقرار شود یا به عبارتی یکی از آن‌ها محدودیت زائد خواهد شد.

توجه: اگر محدودیت به صورت کمتر مساوی باشد باید در سمت راست M جمع زده شود، و اگر محدودیت به صورت بزرگتر مساوی باشد، بایستی M در سمت راست تفریق شود.

حالتی که k محدودیت از بین N محدودیت باید برقرار باشد

مثال: می‌خواهیم از بین پنج محدودیت زیر همواره فقط دو محدودیت برقرار باشد.

$\begin{array}{l} {x_1} + {x_2} + 4{x_3} \le 5\\ 2{x_1} - {x_2} + {x_3} \ge 6\\ 4{x_1} - {x_2} + 4{x_3} \le 9\\ 2{x_1} - {x_3} \le 11\\ {x_1} + {x_2} - {x_3} \ge 6 \end{array}$

پاسخ: برای این منظور محدودیت‌های بالا را به صورت زیر بازنویسی می‌کنیم:

$\begin{array}{l} {x_1} + {x_2} + 4{x_3} \le 5 + M{y_1}\\ 2{x_1} - {x_2} + {x_3} \ge 6 - M{y_2}\\ 4{x_1} - {x_2} + 4{x_3} \le 9 + M{y_3}\\ 2{x_1} - {x_3} \le 11 + M{y_4}\\ {x_1} + {x_2} - {x_3} \ge 6 - M{y_5}\\ {y_1} + {y_2} + {y_3} + {y_4} + {y_5} = 3 \end{array}$

مثال: آیا می‌توانید در همین مسئله آن را طوری مدل‌سازی کنید که از بین 5 محدودیت حداقل 2 محدودیت برقرار باشد؟

${y_1} + {y_2} + {y_3} + {y_4} + {y_5} \le 3$

مثال: آیا می‌توانید در همین مسئله آن را طوری مدل‌سازی کنید که از بین 5 محدودیت حداکثر 2 محدودیت برقرار باشد؟

${y_1} + {y_2} + {y_3} + {y_4} + {y_5} \ge 3$

شکل غیر محدب زیر را در نظر بگیرید و مدل ILP آن را بنویسید.

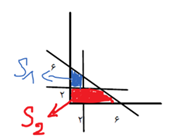
پاسخ: محدودیت‌های هر کدام از فضاهای مشخص شده روی شکل به صورت زیر می‌باشد:

${S_1} = \left\{ \begin{array}{l} {x_1} + {x_2} \le 6\\ {x_1} \le 2\\ {x_2} \ge 2 \end{array} \right.$

${S_2} = \left\{ \begin{array}{l} {x_1} + {x_2} \le 6\\ {x_2} \ge 2 \end{array} \right.$

از بین دو فضا بایستی تنها یکی از آن‌ها برقرار باشد. برای این منظور، محدودیت‌های بالا را به صورت زیر می‌نویسیم:

$\begin{array}{l} {S_1} = \left\{ \begin{array}{l} {x_1} + {x_2} \le 6\\ {x_1} \le 2 + M{y_1}\\ {x_2} \ge 2 - M{y_1} \end{array} \right.\\ {S_2} = \left\{ \begin{array}{l} {x_1} + {x_2} \le 6\\ {x_2} \le 2 + M{y_2} \end{array} \right.\\ {y_1} + {y_2} = 1\\ {y_1},{y_2} \in \{ 0,1\} \end{array}$

در محدودیت‌های بالا، تنها یک متغیر y1 و y2 بایستی مقدار یک بگیرند، پس فقط یک فضا برقرار خواهد بود.

متغیرهایی با مقادیر گسسته

در صورتی که مجموعه مقادیر x به صورت زیر باشد:

$x \in \{ {\lambda _1},{\lambda _2},...,{\lambda _k}\}$

برای فرموله کردن چنین حالتی که فقط بایستی یکی از اعداد مجموعه را شامل شود می‌توان به صورت زیر فرموله کرد:

$\begin{array}{l} x \in {\lambda _1}{y_1} + {\lambda _2}{y_2} + ... + {\lambda _k}{y_k}\\ {y_1} + {y_2} + ... + {y_k} = 1\\ {y_1},{y_2},...,{y_k} \in \{ 0,1\} \end{array}$

مثال: اگر

$|{x_1} - {x_2}| = 0,4,6$

باشد، می‌خواهیم مدل مختلط آن را بنویسیم.

$\begin{array}{l} {x_1} - {x_2} = 0, \pm 4, \pm 6\\ {x_1} - {x_2} = 0{y_1} + 4{y_2} - 4{y_3} + 6{y_4} - 6{y_5}\\ {y_1} + {y_2} + {y_3} + {y_4} + {y_5} = 1\\ {y_1},{y_2},{y_3},{y_4},{y_5} \in \{ 0,1\} \end{array}$

عدد ثابت در تابع هدف

در صورتی که یک هزینه ثابت مربوط به متغیر خاصی در تابع هدف وجود داشته باشد، این هزینه ثابت را ضریب متغیر y که یک متغیر صفر و یک می‌باشد در تابع هدف قرار می‌دهیم.

$MinZ = 2{x_1} + 3{x_2} + \left\{ \begin{array}{l} 6{x_3} + 10 \hspace{5pt} {x_3} \ge 0\\ 0 \hspace{5pt} {x_3} = 0 \end{array} \right.$

به صورت زیر می‌نویسیم:

$\begin{array}{l} MinZ = 2{x_1} + 3{x_2} + 6{x_3} + 10y\\ {x_3} \le My\\ y \in \{ 0,1\} \end{array}$

نکته مهم: در بهینگی به خاطر Min سازی، مقدار حتما صفر می‌شود، اگر مقدار صفر شود. زیرا مدل به دنبال کمینه کردن تابع هدف می‌باشد و تمایلی ندارد که مقدار تابع هدف را افزایش دهد.

یا از کالایی تولید نکنیم و یا اگر تولید کردیم، حداقل lj واحد باشد

$\begin{array}{l} x \le My\\ x \ge {l_j} - M(1 - y)\\ y \in \{ 0,1\} \end{array}$

محدودیت‌های اگر-آنگاه

مثال: می‌خواهیم سه پروژه A، B و C را انجام دهیم. متغیرهای مربوط به آن ها صفر و یک می‌باشند. به طوری که اگر پروژه انجام شود متغیر مربوط به آن یک و اگر انجام نشود متغیر مربوط به آن صفر است.

می‌خواهیم هر سه پروژه انجام شوند

${y_A} + {y_B} + {y_C} = 3$

از بین سه پروژه حداقل دو پروژه انجام شود

${y_A} + {y_B} + {y_C} \ge 2$

دو پروژه A و B یا هر دو انجام شوند و یا هر دو انجام نشوند

${y_A} = {y_B}$

سه پروژه A، B و C یا هر سه انجام شوند و یا هر سه انجام نشوند

$2{y_A} = {y_B} + {y_C}$

انجام A مشروط به انجام B

${y_A} \le {y_B}$

انجام A مشروط به انجام B و C

$2{y_A} \le {y_B} + {y_C}$

دو پروژه A و C ضد یکدیگر می‌باشند

${y_A} + {y_C} = 1$

انجام A مشروط به عدم انجام C

${y_A} \le 1 - {y_C}$

انجام A مشروط به عدم انجام B و C

$2{y_A} \le 2 - {y_B} - {y_C}$

انجام A مشروط به انجام B و C یا هر دو

${y_A} \le {y_B} + {y_C}$

دانلود فایل‌های جزوه

نوع فایل : zip

حجم : 1.35 MB

پسورد : www.optimamooz.com

زمان مطالعه : 3 دقیقه

تاریخ انتشار : 11 فروردین 1403تعداد بازدید : 36نویسنده : optimamooz دسته بندی : برنامه ریزی عدد صحیح

دیدگاه کاربران

عارف 15 فروردین 1403 / 2:57 ب.ظ

پاسخ

بسیار عالی بود
- optimamooz 15 فروردین 1403 / 4:30 ب.ظ
  
  پاسخ
  
  سلام
  تشکر از نظر مثبت شما

ارسال دیدگاه

توسط

^تومان

16 محصول

تعداد محصولات

10 مطالب

تعداد محتوای آموزشی

70 کاربر

تعداد کاربران

دسترسی سریع

درباره ما

ما در آپتیم‌ آموز به دنبال ارائه بهترین منابع و خدمات آموزشی برای دانشجویان هستیم، تا آن‌ها را در رسیدن به اهداف درسی و تحصیلی خود یاری نماییم. با ارائه‌ی محصولات و خدمات متنوعی از جمله فایل‌های مناسب درسی، آموزش‌های درسی تخصصی، برگزاری دوره‌های آموزشی و مشاوره تحصیلی، ما تلاش می‌کنیم تا دانشجویان را در مسیر پیشرفت تحصیلی‌شان همراهی کنیم و به آن‌ها ابزارهای لازم برای بهبود عملکرد و دستیابی به موفقیت فراهم کنیم.

هدف ما از اینجا به شما کمک در بهبود تجربه‌ی آموزشی شماست. با اعتماد به منابع موثق و متنوعی که در اختیار شما قرار می‌دهیم، می‌توانید مسیری موفق‌تر و موثرتر در مسیر تحصیلی خود انتخاب کنید.

آپتیم آموز، همراه شما در سفر آموزشی‌تان است.

ارتباط با آپتیم‌ آموز

ایران، خراسان رضوی، شهر مشهد

09921482241

infooptimamooz.com

کلیه حقوق مادی و معنوی برای این سایت محفوظ می باشد و هر گونه کپی برداری پیگرد قانونی دارد.